Do It Easy With ScienceProg

Embedded Electronics for the Handicapped

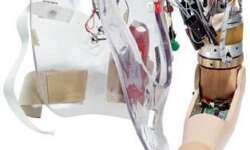
Embedded electronic technology is all around. One may live in a digitized house, ride a car or subway train with embedded sensors and detectors and work using an integrated company network. One can eat lunch in restaurants or play in amusement centres with integrated computers, screens and controllers. Embedded electronics technology is not limited to data transfer, sharing and storage. Many health-care related products also utilize embedded electronics to improve the quality of life. More advanced prosthetic limbs with microprocessors are being developed to bring comfort, stability and balance to be disabled but active members of society.

The Autonomous Flying Ambulance

The autonomous flying ambulance, nicknamed the Mule, created Rafi Yoeli, who used to work for Boeing and Israeli Aerospace Industries. He later founded his own company, Urban Aeronautics, in Yavne, Israel. The Mule is the smaller version of another Urban Aeronautics product, the X-Hawk. The former vehicle has been designed to carry injured military personnel (hence the name “flying ambulance”) out of combat areas. At the same time, the latter is aimed at urban and personal use. Several of Yoeli’s patented inventions are integrated into the Mule, including his VTOL (vertical take-off and landing) vehicle technology and the hybrid drive-powered lift platform. Both the Mule and the X-Hawk, for instance, are classified as VTOL vehicles.

Embedded Electronics and CTX Imaging

CTX imaging is an image capture process that integrates the traditional techniques of computed tomography (CT) scanners and X-rays. The system is still in the prototype stage and is far from small (at present, it’s still as big as one whole room), but Dr. Elizabeth Brainerd of Brown University, who heads the project, hopes that it will become commercial by the first decade of the 21st century. Problems with Previous Technology The two origin technologies of CTX imaging, CT scanner, and X-ray, each had their own problems regarding capturing images. CT scans produce high-quality images that can be viewed in three dimensions, at the cost of speed; subjects being observed have to stay still for up to an hour. X-rays use a fluoroscopy method, which takes images in quick succession, but at the cost of quality; images produced by x-rays can be pieced together to create a video, but they’re of much lower quality and are limited to two-dimensional views. New Features of CTX Imaging CTX imaging is revolutionary because it combines the features of CT scanners and X-rays without compromising either capture speed or image quality. Image capture starts with a traditional X-ray of the subject being observed. The…

Simple signal drawing on graphical LCD routines

During my spare time, I have been playing with graphical LCD. This time I decided to display simple signals that are stored in microcontroller memory. The idea was to read signal values from a lookup table and display waveform on Graphical LCD. To make things more interesting, I divided the LCD screen into four smaller screens to activate them separately and draw signals in them. Graphical LCD is the same old HQM1286404 with KS0108 controller. I have used Proteus simulator 128×64 graphical LCD(LGM12641BS1R), which is based on KS0108. How to implement and connect LCD there was a blog post (Simulate KS0108 graphical LCD with Proteus simulator )about it. I am just going to show main program routine. As I mentioned I have split 128×64 in to four smaller screens like this: So I get four smaller 32×63 screens where I can put different information. To do this, you can think of many ways of implementation. I have chosen a simple solution. I have created a simple structure that holds a currently active window position and size:

How does RFID tag technology works

RFID introduction RFID tagging technology is successfully used among us. Still, we don’t notice them always and do not think about them as they are not noticeable because we do not have to take any actions to transfer or read any information from RFID tags. But probably everyone notices in big supermarkets, book stores two parallel frame antennas and thicker labels on products you buy, or maybe you have an RFID entrance card at your work. So let’s see how this technology works. RFID is a so-called Radio Frequency Identification system that consists of two main parts: transmitter and receiver. The labels, access cards, and even passports in some countries have RFID transponders integrated. These transponders are called tags. Each tag has information programmed in it. A reader can read this information via the Radio Frequency link. Tags can be very miniature, like thicker paper sheets. The simplest ones have only an antenna and diode. These tags only reflect signals incoming from transmitters. These are tags that are used in supermarkets and other places for securing goods from stealing. If the signal is reflected, an alarm is triggered. When the seller scans the tag, it is electrically destroyed to trigger…

Interfacing microcontrollers to external devices

There can be any external device that may be connected(interfaced) to the microcontroller. They may be for control input like buttons, keypads, touch, or information output, e.g., display, sound, motor, relay, and modem. Also, output devices may be further chips like transmitters, frequency generators, memory. Interfacing with chips is not that hard because most of all (especially digital ones) are TTL level compliant that allows connecting chips one to another directly. Otherwise, there are TTL level converter chips if needed â€“ like RS232 to TTL converter MAX232 chip. Let’s take a simple device LED. Probably many of you are thinking that there is nothing easier than connecting LED to the microcontroller. Yes, it’s true. Considering AVR microcontrollers, Led can be connected directly to port pin via limiting resistor either as a source either as drain because the chip can provide enough current to light diode without damaging the port. But what if you need to connect like 10 LEDs when each requires, let’s say 20mA. The total current would be 200mA. No tall microcontrollers can provide such power directly without damaging the port. The simplest way to avoid this problem is to use LED via amplifying transistor.

DIY pulse soldering iron

The biggest benefit I see when working with a pulse soldering iron is speed and effectiveness. Of course, when you don’t work, it stays cool; this means it saves energy, doesn’t evaporate poisonous steam, and there is no risk of accidentally burning yourself. Well, this one even has a light source for a better view when soldering. If you like to hack things, you may try this challenge on building a pulse soldering iron. This iron may be powered from a 220V supply and consumes about 70-100W of power. Efficiency reaches about 50%. The heating time takes 5 seconds while cooling to 50ºC takes about 15 seconds. Soldering iron may be used in various tasks, including repairing home appliances, replacing electronic parts, etc.

Kick start guide to start working with Programmable Logic Devices from Altera

Probably everyone knows what logical IC’s and how to use them in the design are. But if the design is more complex, electronics enthusiasts are more likely to choose microcontrollers as they minimize the count of external components. But the problem is that not everything is possible with microcontrollers. They have many disadvantages when a fast response to input signals is needed. Microcontrollers execute operations one by one in sequence (conveyor). So output results will occur after some number of clock cycles. One way is to use hard logic IC’s. But when complexity grows – the number of IC packages also increases. This way design board becomes tremendous. So where programmable logic devices (PLD) comes to help. CPLD devices have many base elements (gates) without strict electrical interconnection. So designer can program these connections to combine any logical combination. Programmable logical devices allow the construction of any logical device, including counters, triggers, etc. The limit is only the number of base elements and connection lines. So it is better to start with learning tools that allow the construction of logical circuits, simplify them, and avoid many mistakes. One of them is MAX+plus II BASELINE and CPLD from ALTERA. This software…

DIY simple band-pass filter

This filter was designed to filter the 1kHz frequency of the telemetric signal from environmental noise. The filter itself is straightforwardly built with acceptable electronic parts worldwide. This filter can be used in any circuit because of its simplicity. The circuit contains a minimal amount of parts, including one general-purpose NPN transistor with coefficient 50…70 and more. Such filter blocks may be connected in series directly one to another(second IN first OUT). This way, filter gain may increase up to 1,2…2.

Testing AVR universal bootloader on Atmega128

After the project source code is developed, there is always a need to flash it to the microcontroller. There are a few ways to program AVR microcontrollers. Usually, we used to flash AVR’s with an ISP adapter (or another programmer) that is not always handy, especially when designing a device for the end-user who doesn’t have an ISP adapter or doesn’t know much about flashing MCU. So it is better to flash a bootloader program AVR MCU once with a programming adapter and later load firmware interactively when starting AVR. The bootloader allows updating the firmware without a programmer and enables different programs for different purposes depending on the situation flexibly. But enough about this. So my purpose today is to test AVR universal bootloader, which Shaoziyang is developing. He aimed to create a universal bootloader that works on different AVR microcontrollers with minimal code modifications. Bootloaders you can find on the Internet are mostly available for particular microcontrollers, and nobody wants to do a lot of modifications to adapt to different MCU when needed. This AVR universal bootloader can support most AVR microcontrollers (Mega series), which have the self-programmable capability, boot section, and UART. If the device has many…