AVR internal oscillator jitter research
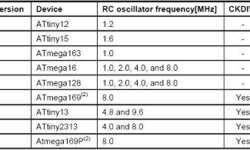
If you go to the AVR site and open an AVR application note AVR053, you will notice different RC oscillators installed into AVR chips during history. In the table, you can see tunable oscillator versions and their features. Simply speaking, each new version of the oscillator introduces better features and improvements. But is it true? ChaN has done exciting research on this oscillator version. He tested the output signal with fixed width and measured timing fluctuations of it. And he found out that the RC generator frequency slowly fluctuates during the time. Of course, RC oscillator fluctuations are not a problem as this type of clock source isn’t stable. In time-critical applications, it is better to use crystals. But the most exciting thing is that newer versions of tunable oscillators were generating much more jitter than older ones.