This pilot study is intended to investigate possibilities of skin nevus imaging using digital still image camera. The main objective is to develop a dermatology image interpretation method, which enables the looking on the skin lesions and nevus from the optical background of skin colouration. Kubelka-Munk calculation method for light transport and reflection from multilayered, complex media is applied to model light reflection spectra of skin. Calculation of model shows that red, green, blue and infrared colours lighting is satisfactory to access distribution of comparative estimates of the following skin parameters: volume fraction of melanin in the epidermal layer, the volume fraction of haemoglobin in the dermal layer, presence of dermal melanin and thickness of the papillary layer. Performance of image processing method on fourteen samples of images of common melanocytic nevi, dysplasia melanocytic nevi, Spitz nevus, thrombotic hemangioma and surrounding healthy skin were made.
Skin spectral properties
Understanding how light interacts with skin can assist in designing physics-based dermatological image processing. The key is understanding how light interacts with skin tissue. The skin consists of different layers with different spectral properties.
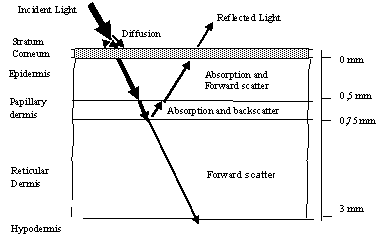
Fig 1. Skin model and its physical view When incident light is applied to skin layer, it is absorbed, and another part is scattered. The main layers of skin areas as follows: Stratum cornea it practically doesn’t absorb light, but diffuses it; Epidermis consists of cells producing pigment melanin. Melanin strongly absorbs light wavelengths towards the ultraviolet part; Dermis is next to the skin layer, consisting of collagen fibres. It can be split into two sublayers: Papillary dermis and dermis itself. The papillary dermis consists of the high density of collagen fibbers who is strong scatterer of light.
Implementation of skin spectral model
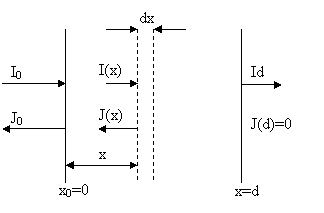
Skin is modelled as two light fluxes through three-layer media. As Kubelka Munk theory says, Incident light flux is resolved into two fluxes: one is directed into deeper layers, and other is oppositely directed because of backscattering.
Because of the layered skin structure, there are multiple reflections. They can be solved as an infinite sum:
For the N layer system, R1,2…n and T1,2..n are expressed as recursive equations:
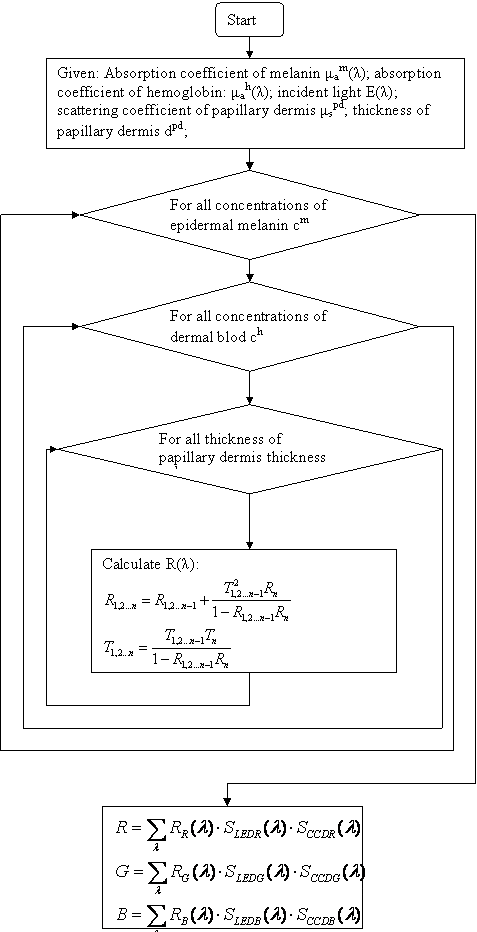
The primary model requirement is that light has to be scattered. Stratum cornea is supposed as scattering filter. According to earlier studies skin can be characterized as follows:
- Epidermis, depending on wavelength can be described with melanin absorption coefficient μam(λ) and melanin concentration cm;
- The papillary dermis can be described with haemoglobin absorption coefficient μah(λ), haemoglobin concentration ch, collagen scattering coefficient μspd and collagen layer thickness dpd;
- The dermis can be described with scattering coefficient μsrd and thickness of layer drd. Using those parameters, the model of skin was calculated, which shows reflected light R(λ) dependency on skin parameters and wavelengths of light:
Ranges of volume fraction of melanin cm –are in range for normal healthy skin: 0,01 – 0,5; ch – hemoglobin volume fraction coefficient, in model: 0,001 – 0,05.
RR(λ), RG(λ), RB(λ) are reflectance spectra for red, green and blue illumination. SLEDR, SLEDG, SLEDB – light source spectral characteristics; SCCDR, SCCDG, SCCDB – CCD sensor sensitivity to light wavelength.
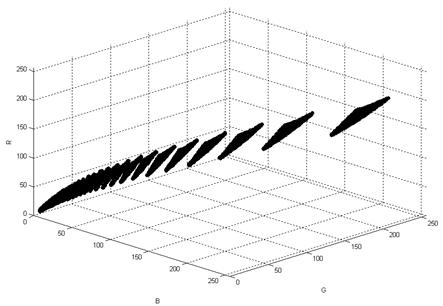
After these calculations, we get one RGB vector pointed to one point in RGB space for one independent set of parameters:
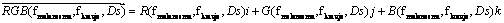
All vector values is displayed in RGB space drawing a color surface of all available healthy skin colors
This model is valid for all healthy skin; there is no melanin present in the papillary dermis. This model does not depend on race or even on sunburn degree.






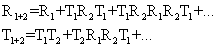
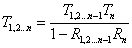
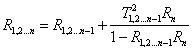
Me… Is it anything you would like to ask?
who is the writer of this note ?
The model is wrong.. does not account for absorbtion of efferent light in the tissue.. a 2nd order effect. You should be able to do this by calculus anyway. Look up extinction lengths.