Recently I’ve been reviewing wavelet transform. I think some points are worth sharing. In this first post, I would like to mention the basics of wavelet transform and its main features.
A probably most important question that comes to mind is why we need another transform when we already have Fourier transform. The answer lies in the signals that we want to analyze. If we take any periodic signal that is stationary (e.g., Pulse train) then Fourier transform is the right tool because its frequency components don’t change in time. Let’s take another case when the signal changes in time (chirp signal).
Classical Fourier transform cannot determine frequency components of such signal because it doesn’t carry any information about signal time scale. Of course, it is possible to cheat with Short Time Fourier Transform (STFT) when the signal is analyzed in short chunks, but again there is a problem of resolution – the shorter chunks give better time resolution, and longer – better frequency resolution. You can find more info on this by looking for Heisenberg’s Uncertainty Principle. So there is always a tradeoff between both. A fundamental limitation of Fourier transform is in its base function, which is a cosine wave. Its nature tells that it is meant to analyze periodic signals.
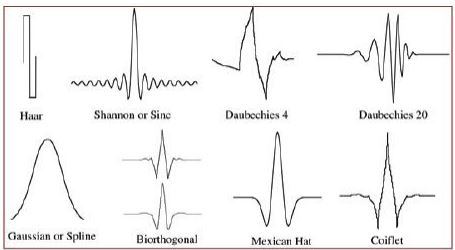
This is where Wavelet Transform (WT) enters. Its base function is called a wavelet which is short duration function with specific center frequency.
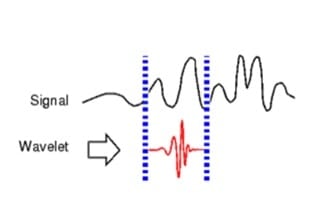
There are many types of wavelet functions that have their unique names. Since wavelets are limited in time, analyzed signals are deconstructed into wavelet domain which carries time and frequency information. Resolution problem is solved by its nature – by scaling and shifting operations during transform process. Wavelet transform goes as follows: short wavelet is shifted along analyzed signal where scalar multiplication (similarity) is performed at each point.
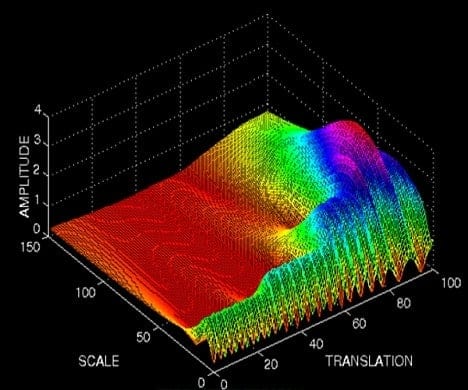
Then wavelet scale is changed, and the process is repeated until whole spectrogram is generated. Wavelet spectrogram can be displayed on the nice 3D graph where one axis represent scale, another shift (translation), and third – amplitude.
As you can see, the low scale represents high frequency component change along translation axis, while large scale gives low frequency data.
Next time we will get in to wavelet transform practical uses.