Probably you’ve heard about Naive Bayes classifier, and likely used in some GUI-based classifiers like WEKA package. This is a number one algorithm used to see the initial results of classification. Sometimes surprisingly, it outperforms the other models with speed, accuracy and simplicity.
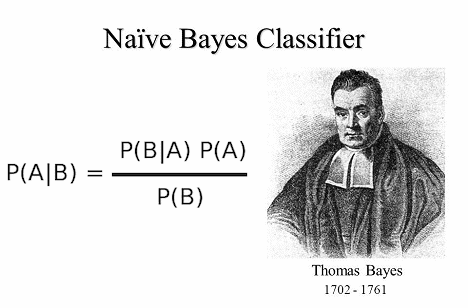
Lets see how this algorithm looks and what does it do.
As you may know algorithm works on Bayes theorem of probability, which allows to prediction the class of unknown data sets. Hoe you are comfortable with probability math – at least some basics.
Naive Bayes basics
Naive Bayes is a classification algorithm that is commonly used in machine learning and natural language processing. It’s based on Bayes’ theorem, which is a statistical rule that describes the relationship between conditional probabilities.
In the context of Naive Bayes, the algorithm works by calculating the probability of a data point belonging to a particular class based on the probabilities of each feature in the data point. The algorithm is called “naive” because it assumes that each feature is independent of all the other features, even though this may not be true in practice.
Let’s say we want to use Naive Bayes to classify emails as either spam or not spam based on their content. We would start by collecting a dataset of emails, some of which are labeled as spam and some of which are labeled as not spam. Each email in the dataset would have a set of features, such as the frequency of certain words or the length of the email.
To train the Naive Bayes classifier, we would calculate the probabilities of each feature in each class (spam or not spam). For example, we might calculate the probability that an email is spam given that it contains the word “viagra” and the probability that an email is not spam given that it contains the word “hello.” We would also calculate the probabilities of each feature occurring in the dataset overall.
Once we have calculated these probabilities, we can use them to classify new emails as either spam or not spam. We do this by calculating the probability of each class given the features of the new email, and choosing the class with the highest probability.
For example, if we receive a new email that contains the word “viagra” and has a length of 1000 characters, we would calculate the probability that the email is spam given these features, using the probabilities we calculated during training. We would also calculate the probability that the email is not spam, given these features. The class with the higher probability would be chosen as the predicted class for the email.
Naive Bayes algorithm is convenient on massive data sets because it’s fast, simple, and accurate when compared to other classification algorithms.
Let’s dig into some math to understand the basics.
Bayes algorithm is based on the posterior probability that combines previous experience and the likelihood of an event. To understand all of that, let us look at a simple example. Below you can see whether data set with two features (temperature, humidity) and class (play). We will want to build a Naive Bayes predictor, which would tell if weather is suitable for playing golf or not in current conditions.
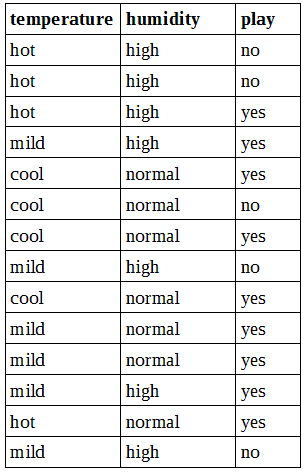
We would like to know if temperature cool, along with high humidity, is suitable for playing golf.
According to Bayes theorem, we need to calculate the posterior probability
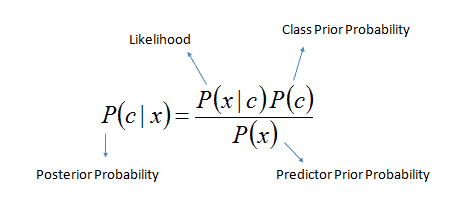
Or simply we calculate in expanded form:
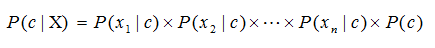
We need to calculate it for each class and then compare the results to find which gives the higher score.
Let’s get to our data and go through it step by step.
Since we want to classify temperature cool and humidity high, we need to find following probabilities:
P(cool|yes), P(high|yes),
P(cool|no), P(high|no),
P(yes), P(no),
optionally we might want to calculate P(cool) and P(high); as you will see, this isn’t necessary for basic classification.
P(cool|yes) = (likelihood of cool given yes) / (total number of yes) = 3 / 9 = 1/3;
P(high|yes) = (likelihood of high given yes) / (total number of yes) = 3 / 9 = 1/3;
P(cool|no) = (likelihood of cool given no) / (total number of no) = 1/5;
P(high|no) = (likelihood of high given no) / (total number of no) = 4/5;
P(yes) = (number of yes) / (total number of play) = 9/14;
P(no) = (number of no) / (total number of play) = 5/14;
also lets calculate P(cool) and P(high):
P(cool) = (number of cool) / (total number of temperature) = 4/14;
P(high) = (number of high) / (total number of humidity) = 7/14 = 1/2;
To get the answer we then calculate two posterior probabilities and compare results:
As we can see that 0.5 > 0.4, we can predict that temperature cool and high humidity is suitable to play golf.
Once you get used to it, Naive Bayes become really easy algorithm to implement. Due to its simplicity, it can be implemented in real-time predictors, and works well with multiple classes that leads to spam filtering, and text classification.





