A Second-order DSP filter is more complex than a first-order filter. There is one more delay block (z-1) added. Function diagram of second-order DSP filter.
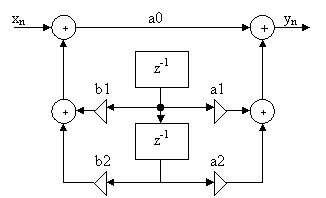
The equation for second order DSP Filter can be written as follows:
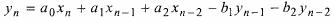
And transfer function expressed in Z transform would be:
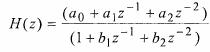
There can be two particular cases of filter. If we can write a general expression of filter like this:
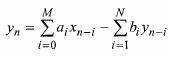
Then:
1) When N=0, we get a non-recursive digital filter (FIR – Finite Impulse Response). This is a simple sum of a finite number of samples. In other words – averaging filter.
2) When N>0, we get a recursive filter. This filter (IIR – Infinite Impulse Response) has feedback where output samples are branched to input together with input samples. This type of filter has stability issues and so on.
The general form of transfer function may look like this – applies to all filter types:
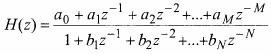
What about the realization of the filter? Using digital filters in embedded systems is a critical issue. The sampled signal is forwarded to filter input as x(nT) queue, and output is y(nT) due to the digital processing of the signal. Speed of processing may be defined as minimal clock period Tmin of sampled input signal x(nT) or by frequency band Fmax=1/(2Tmin) of signal (according to Nyquist identity). The lower Tmin is – the higher Fmax – the speed of DSP processing. The main target of DSP processing usually is the real-time processing of wideband signals.
Universal microcontrollers are almost useless in higher speed signal processing. To make it effective, there are needed parallel modules in microcontrollers, but universal microcontrollers can perform one task simultaneously. Another situation is with DSP processors. They have the ability to parallel some instructions and increase the speed of critical parts of algorithms.
The most effective DSP can be done using FPGA. There all commands can be performed in parallel and at high speed. I am not going too deep in this as this needs a separate analysis thread.





