Impulse signal can be represented as:
d[n] = 1, if n=0
d[n] = 0, otherwise
it can also be written like d=[1,0,0,0,…]
Impulse Response
The impulse response h(n) is the response of filter L() at time n to unit impulse occurring at time 0.
h(n)=L(d(n))
Let’s see how a discrete system can be described when impulse response is known
We know that:
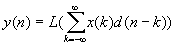
In the linear system this can be written as follows:
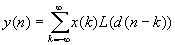
Because h(n-k)=L(d(n-k))
Then:
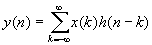
What do we get? Its impulse response can describe a linear system. The last expression is called convolution. This is the heart of DSP Filtering.
To write this sum in the more convenient matter is assumed that:

Matlab example
Matlab example:
% Plot an unit impulse signal
n = -7:7;
x = [0 0 0 0 0 0 0 1 2 3 0 0 0 0 0];
subplot(4,2,1);
stem(n, x);
limit=[min(n), max(n), 0, 5];
axis(limit);
title('Input x[n]');
subplot(4,2,3);
x0=0*x;
x0(8)=x(8);
stem(n, x0);
axis(limit);
h=text(0, x0(8), 'x[0]');
set(h, 'horiz', 'center', 'vertical', 'bottom');
subplot(4,2,4);
y0=0*x;
index=find(x0);
for i=index:length(n)
y0(i)=x0(index)*exp(-(i-index)/2);
end
stem(n, y0);
axis(limit);
h=text(0, x0(8), 'x[0]*h[n-0]');
set(h, 'vertical', 'bottom');
subplot(4,2,5);
x1=0*x;
x1(9)=x(9);
stem(n, x1);
axis(limit);
h=text(1, x1(9), 'x[1]');
set(h, 'horiz', 'center', 'vertical', 'bottom');
subplot(4,2,6);
y1=0*x;
index=find(x1);
for i=index:length(n)
y1(i)=x1(index)*exp(-(i-index)/2);
end
stem(n, y1);
axis(limit);
h=text(1, x1(9), 'x[1]*h[n-1]');
set(h, 'vertical', 'bottom');
subplot(4,2,7);
x2=0*x;
x2(10)=x(10);
stem(n, x2);
axis(limit);
h=text(2, x2(10), 'x[2]');
set(h, 'horiz', 'center', 'vertical', 'bottom');
subplot(4,2,8);
y2=0*x;
index=find(x2);
for i=index:length(n)
y2(i)=x2(index)*exp(-(i-index)/2);
end
stem(n, y2);
axis(limit);
h=text(2, x2(10), 'x[2]*h[n-2]');
set(h, 'vertical', 'bottom');
subplot(4,2,2);
stem(n, y0+y1+y2);
axis(limit);
title('Output y[n] = x[0]*h[n-0] + x[1]*h[n-1] + x[2]*h[n-2]');
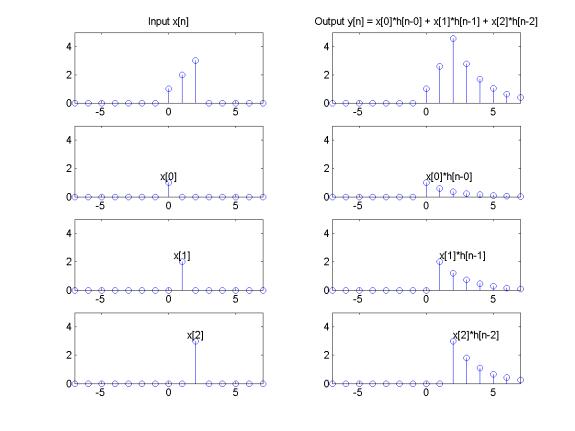
As you can see if the input queue has N samples, impulse response has M after convolution there will be total N+M-1 samples.





