Power sources for AVR
Power sources for AVR are very important part in projects. Avery circuit has to be powered from some source like battery or from AC adapter 110V/220V. Using batteries is more convenient way to power the microcontroller projects as the circuits are simpler and constructed devices become portable.
There are many types of batteries in shapes and sizes or capacities. So when choosing battery you should consider many factors:
- Capacity – this is very important parameter measured in mA/h. This parameter defines how long your microcontroller project will be working before recharging or replacing batteries. Rule is simple – as bigger battery capacity as longer your circuit will be working, but in other hand your project may become more expensive or even heavier because of bigger batteries.
- Second parameter is battery Voltage. If Voltage of battery is to small for tou circuit, youll have to connect several batteries in series.
- Other is Expirity date. You don’t want your battery energy leakage or become obsolete because of this.
- Working temperature. If your project will be working in more extreme temperatures – heat or cold, then you should consider this.
- And the last parameter would be chape, size and weight. If your project is flying model control, then you will look for light, small and capacious battery.
If you decide to power your Atmega project from AC line, then you need to transform your line voltage to near 5V and stabilize it using voltage regulator like 7805.
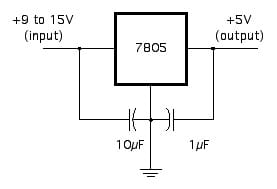
This regulator outputs stabilized 5V up to 1A. If you don need more than 100mA you should choose 78L05 chip.
In some cases if your project is connected to computer port and circuit requires small current you can power circuit directly from port. For instance usually circuit connects to LPT using 3 wires and other lines as outputs can serve as power source by writing to these lines value “1â€.
Similar situation is with RS232. Just there you need to put voltage regulator or zener diode as voltages are not in 0 – 5V range. You should connect more then 10uF capacitor in parallel to zener diode.
Just remember that regardless the power source you use you should connect like 0.01…0.1uF capacitor between power line and ground in order to filter noises. This applies to any digital IC in circuit.
Blogsphere: TechnoratiFeedsterBloglines
Bookmark: Del.icio.usSpurlFurlSimpyBlinkDigg
RSS feed for comments on this post | TrackBack URI for this post
New on WinAVR Tutorial
Running TX433 and RX433 RF modules with AVR microcontrollers,Sometimes in embedded design you may want to go wireless. Might be you will want to log various readi …Programming AVR ADC module with WinAVR,Most of AVR microcontrollers have Analog to Digital Converter (ADC) integrated in to chip. Such solut … |
New on WinARM Tutorial
What are differences between WinARM and WinAVR,Everyone who is working with AVR microcontrollers knows this powerful tool – WinAVR (http://win …LPC2000 watchdog timer,As in all microcontrollers watchdog timers purpose isto reset microcontroller after reasonable amount … |
