Electrical signal power and energy calculations by example

In electronics and signal processing, you have to deal with electrical signals. In many cases, you may need to calculate signal power and energy.

Power and energy for DC

In a standard situation, when DC power supply is applied to a known resistor or another device like an LED motor you can calculate its power very easy by applying Ohms law:

$P = \frac{U^{2}}{R}$

If we run this device for time T then we can calculate total energy used:

$E = T\cdot \frac{U^{2}}{R}$

In some cases, you may not know the resistance of your circuit. In this case, you can measure the current flow. So your power formula can be transformed by using same Ohms law:

$P = U\cdot I$

So, for instance, if you connect your circuit to the 3V power supply and measure that it uses 0.5A of current, you can calculate the instant power usage:

$P = 3\cdot 0.5 = 1.5W$

And the energy used during one hour:

$E = 1\cdot 3\cdot 0.5 = 1.5Wh$

Variable signal power and energy applied to load

Things get a bit more complicated when signal current isn’t continuous DC. In signal processing applications, the term signal power and signal energy are introduced. The idea is practically the same as in DC. But since current (or voltage) changes in time, it is written as v(t) and i(t). for instance, for periodic harmonic signals, we can write

$v(t) = V\cdot cos(\omega \cdot t)$ .

To calculate signal power, we can apply Ohms formula from above.

This way, we can calculate instantaneous power of the signal at any time: $p(t) = \frac{v(t)^{2}}{R}$ .

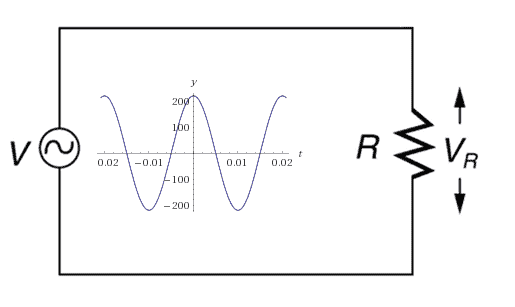
Let’s say our voltage is periodical $v(t) = 220cos(2 \pi f t)$ where f = 50Hz. And we apply this voltage across 100Ω resistor. At 20 seconds time, we can calculate momentary power usage:

$p(t) = \frac{v(t)^{2}}{R}=\frac{(220cos(10000 \pi ))^{2}}{100} = 484W$

If we want to calculate energy loss during 100s we need to integrate the power in period from 0 to T:

$E = \int_{0}^{T} p(t)dt = \frac{1}{R}\int_{0}^{T}v^2(t)dt$

I know – everyone hates integrals, but this is how math works. In many cases, you don’t need to integrate manually – just place formulas into one of the packages like WolframAlpha, and you will get the answer immediately.

Let’s apply energy formula to our signal:

$E = \frac{1}{100}\int_{0}^{100}(220cos(100 \pi t ))^{2}(t)dt = \frac{121(200\pi))}{5\pi}=672.22Wh$

!dont apply 220V to 100Ω resistor.

When we know the energy consumed during time T, we can calculate average power over a period of time:

$P_{avg} = \frac{E}{T} = \frac{1}{RT}\int_{0}^{T}v^2(t)dt$

And with our previous example, we calculate average power:

$P_{avg} = \frac{672.22Wh}{0.03h} = 22407W = 22.4kW$

!dont apply 220V to 100Ω resistor.

I hope you get the idea what’s going on here.

Signal power and energy

In signal processing for, it is agreed to eliminate the resistance parameter from equations by making it equal to 1 (R = 1). Also, instead of v(t), usually, signals are expressed as s(t). Thus we can express signal energy as follows:

$E = \int_{0}^{T}s^2(t)dt$

Signal power:

$p(t) = s^2(t)$

And average power over the time period:

$P_{avg} = \frac{E}{T} = \frac{1}{T}\int_{0}^{T}s^2(t)dt$

Finite and infinite signal energy

There is one more important matter about signals. They can be the finite length or infinite. If we need to find the power of an infinite signal, we need to find its average power overall time:

$P_{avg} = \lim_{T\rightarrow \infty }\frac{1}{T}\int_{-T/2}^{T/2}s^2(t)dt$

Power of infinite signal can be calculated as follows:

$E = \int_{-\infty}^{\infty}s^2(t)dt$

For some signals, power and energy can be found by intuition. For instance, let us take a step signal:

We can see that the energy of the signal grows to infinity when time also goes to infinity. Average power on the other hand, is 0.5W.

In another case, we have a sinusoidal signal:

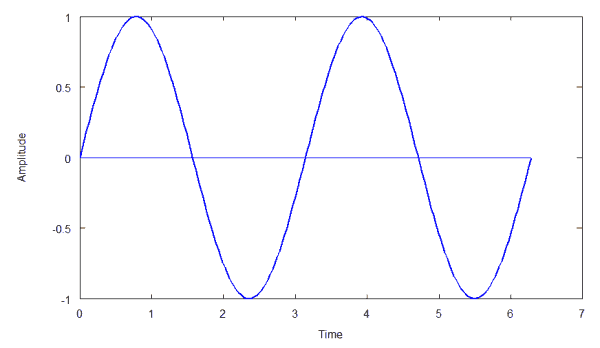
If we applied the formulas above, we would get signal energy = ∞ and average power = 0.5W.

And lastly, fascinating case – sinc signal:

$s(t) = sinc(t) = \frac{sin(t)}{t}$

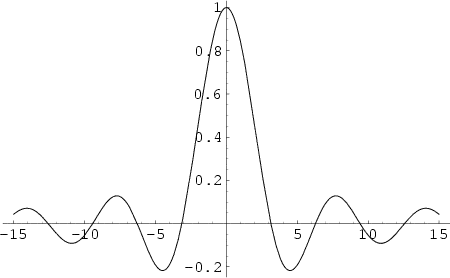
signal energy = π and average power = 0W.

The RMS

If we take the square root of average power then we get root mean square (RMS) of the signal:

$RMS = \sigma_{s} = \sqrt{P_{avg}} = \sqrt{\lim_{T\rightarrow \infty }\frac{1}{T}\int_{-T/2}^{T/2}s^2(t)dt}$

For instance, if we get sine wave average power equal to 0.5W, then RMS:

$RMS = \sigma_{s} = \sqrt{0.5} = 0.707W$

What does RMS mean in practice?

In practice, RMS (root mean square) is a mathematical calculation used to determine the practical value of a time-varying signal. It is often used to calculate the average power of an AC (alternating current) signal or the amplitude of a waveform that is not purely sinusoidal.

For example, if you have an AC signal with a peak amplitude of 10 volts, the RMS value of the signal would be approximately 7.07 volts. This is because the RMS value takes into account the changing amplitude of the signal over time rather than just the maximum or peak value. In the case of an AC signal, the RMS value is proportional to the average power of the signal, making it a valuable metric for determining the amount of energy being transferred by the signal.

In general, RMS is a helpful measure of the “strength” of a signal, as it provides a single value that takes into account the entire waveform over time. It is commonly used in fields such as electrical engineering, signal processing, and physics to describe the behavior of time-varying signals.

If you have sine signal amplitude 220V, then it’s RMS = 220·0.707 = 155.54V.