Ultrasound waves are acoustic pressure waves that interact with propagation media. Ultrasound visualization is typically based on wave reflectance from regions with different acoustic properties. When a wave meets different acoustic media, part of it transmits further while others reflect. This happens due to different acoustic impedance. The ration between reflected and transmitted energy purely depends on the difference in acoustic impedance in both regions.
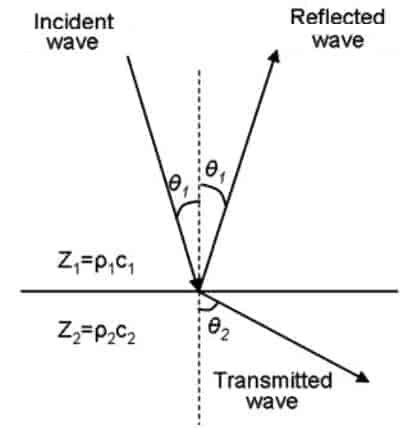
As you can see each material can be characterized by its acoustic impedance Z which is equal to ultrasound speed v and material density r.
Z = r∙ v;
Acoustic impedance units are MRayl [10-6 kg∙s-1∙m-2]. If we know acoustic impedances Z1 and Z2 of two regions crossed by ultrasound waves, we can calculate reflectance coefficient R:
And Transmit coefficient T:
As you can see if there is a bigger difference between the two acoustic impedances, the more wave energy gets reflected. For instance, air acoustic impedance is much lower than liquid or human tissue; this is why a water-based gel is used to avoid an air gap between measured media. Otherwise, almost all ultrasound energy would be reflected due to a large difference in acoustic impedances. The gel ensures that practically all ultrasound energy is transmitted to tissue.
When ultrasound wave is transmitted to different impedance area, it refracts according to Snell law. According to it incident wave angle and refracted wave angle ration are proportional to speed ratio in both media:
These are very basics of wave propagation and applies to other wave phenomena like optics.
Ultrasound attenuation
Attenuation is another important feature of wave propagation. In all cases, a wave travelling through media is attenuated. This is because media absorbs of energy which is converted to heat, so in its way, ultrasound wave loses its energy and so amplitude drops. Mathematically attenuation can be modelled using the exponential equation:
P0 – is the wave energy at the entry point, x – is the point of interest; a – attenuation coefficient. Speaking of the attenuation coefficient, it isn’t constant value. It depends on the frequency a = H(f) – the higher wave frequency, the higher attenuation coefficient value. If we take biological tissue, attenuation can be modelled with two mechanical components – elasticity and viscosity. Elasticity is modelled with spring, while viscosity with damper.
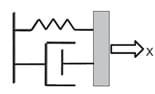
Both mechanical components together create a viscoelasticity effect which works similar to the car shock absorber. When shock frequency is low absorber dampens and practically copies the surfaces, but when car speed is high, the absorber is stressed at a high rate and elasticity takes over the springy action. If you touched shock absorber after intense driving on the non-even surface, you would see that it becomes hot. So similar situation is with ultrasound propagation. If high-frequency ultrasound is transmitted, it gets attenuated more intensively due to the viscosity of tissue. So practically in all ultrasound visualization devices, there is a time gain compensation feature installed which compensate the signal level overall depth of scan.





