Sampling is a process when a series of discrete samples represent the continuous-time signal. At the same time, the reconstruction is the reverse process when these samples recreating adequate continuous-time signals. Bellow, the overall process is illustrated.

Sampling is a process when the continuous-time signal is recorded every T seconds by multiplying by an impulse train.
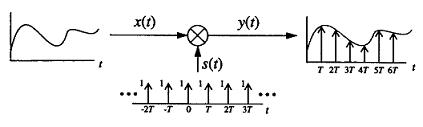
Suppose the signal is sampled in the frequency domain. For this, we need the signal transformed into the frequency domain. The frequency spectrum has to be band-limited. The impulse train after transformation becomes an impulse train with scale in heigh 1/T. Multiplication in the time domain becomes a convolution in the frequency domain. After convolving, the signal is scaled and shifted. The signal in the frequency domain becomes periodical.
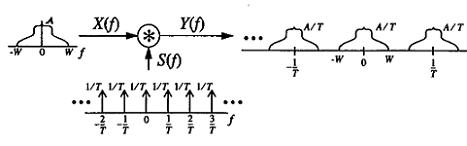
To reconstruct the signal x(t) from the sampled spectrum, first, we need to extract the original spectrum. This ideal filter is needed to take a single spectrum from the spectrum signal train. Low pass filter fill cut other copies of the spectrum. The filter should have cut off at f=±1/(2T) and Gain of T:

After this, reconstruction can be done. The ideal filter in the frequency domain is a sinc function in the time domain. This means that multiplying spectra by the box in frequency domains means convolving with a sinc function in the time domain. Because y(t) is a series of impulses, then reconstructed x(t) is a superposition of scaled and shifted sinc functions:

The fundamental result is that equally spaced samples can completely discretize any band-limited signal. And remember that sampling frequency has to be at least two times bigger than the band limit of signal to avoid alias (overlap) of sampled signal spectra. Otherwise, the reconstruction of the original signal becomes impossible.


Discrete signals are sampled from analog signals. So you get samples in fixed time intervals. Discrete signal is as sequence of numbers.